अदिश भौतिक राशियाँ - वे भौतिक राशियाँ जिन्हें पूर्णतः व्यक्त करने के लिए केवल उनके परिमाण की आवश्यकता होती है , अदिश राशियाँ कहलाती हैं । उदाहरण - दूरी , चाल , समय , कार्य , ऊर्जा आदि
सदिश भौतिक राशियाँ - वे भौतिक राशियाँ जिन्हें पूर्णतः व्यक्त करने के लिए उनके परिमाण के साथ - साथ दिशा की भी आवश्यकता होती हैं , सदिश राशियाँ कहलाती हैं । उदाहरण – विस्थापन , वेग , त्वरण , बल , संवेग आदि ।
सदिश राशियाँ संयोजन के सामान्य नियमों का पालन नहीं करती । इनका संयोजन त्रिभुज नियम , समान्तर चतुर्भुज नियम तथा बहुभुज नियम से किया जाता है ।
सदिश राशि का ज्यामितीय निरूपण - एक सदिश राशि को ज्यामितीय रूप से व्यक्त करने के लिए सदिश राशि की दिशा में एक सीधी रेखा खींची जाती है तथा दिशा के अनुदिश इस पर तीर का चिन्ह लगाया जाता है । इस रेखा की लम्बाई , उचित पैमाना मानकर सदिश राशि के परिमाण के अनुपात में ली जाती है । यदि एक साथ एक से अधिक सदिशों को व्यक्त करना हो तो सभी राशियों के लिए एक ही पैमाना प्रयुक्त करते हैं ।
जैसे - एक वस्तु पर कार्यरत
| → |
| F |
 |
| सदिश राशि का ज्यामितीय निरुपण |
सदिश राशियों के संयोजन का समान्तर चतुर्भुज नियम - दो या दो से अधिक सदिशों के प्रभाव को एक ही सदिश द्वारा व्यक्त करना , सदिशों का संयोजन कहलाता है । प्राप्त सदिश , इन सदिशों का परिणामी सदिश तथा जिन सदिशों का संयोजन किया गया है वे इस परिणामी सदिश के घटक कहलाते हैं ।
समान्तर चतुर्भुज नियम - इस नियम के अनुसार “ यदि दो सदिशों को एक समान्तर चतुर्भुज की दो आसन्न भुजाओं के रूप में व्यक्त किया जाये तो समान्तर चतुर्भुज का इन दो आसन्न भुजाओं के कटान बिन्दु से निकलने वाला विकर्ण , परिमाण तथा दिशा में , दोनों सदिशों के परिणामी सदिश को व्यक्त करता है । ”
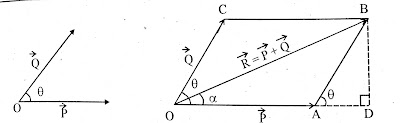 |
| सदिश संयोजन का समान्तर चतुर्भुज नियम |
परिणामी सदिश का परिमाण R = √P2 + Q2 + 2PQ cosθ
जहाँ θ ,
| → |
| P |
| → |
| Q |
| → |
| R |
| → |
| p |
तीन समतलीय सदिशों का संतुलन - किसी एक ही बिन्दु पर कार्यरत ( संगामी ) तीन समतलीय सदिश
| → |
| P |
| → |
| Q |
| → |
| S |
| → | → | → | |||
| P | + | Q | + | S | = 0 |
अर्थात्
| → | → | → | |||
| S | = -( | P | + | Q | ) |
| → | → | |
| S | = - | R |
| → | → | → | ||
| R | = | P | + | Q ) |
अर्थात् किन्हीं भी दो सदिशों का परिणामी सदिश , तीसरे सदिश के समान परिमाण का तथा विपरीत दिशा में हो तो तीनों सदिश परस्पर संतुलन में होते हैं । परस्पर संतुलन की स्थिति में
| → | → | |
| S | = | R |
या
1 . अदिश राशियों को परिभाषित कीजिए ?
उत्तर - वे राशियाँ , जिन्हें पूर्णतः व्यक्त करने के लिए केवल परिमाण की आवश्यकता होती है , अदिश राशियाँ कहलाती हैं ।
प्रश्न 2 . सदिश राशियों को परिभाषित कीजिए ।
उत्तर - वे राशियाँ , जिन्हें पूर्णतः व्यक्त करने के लिए परिमाण के साथ - साथ दिशा की भी आवश्यकता होती है । सदिश राशियाँ कहलाती हैं ।
प्रश्न 3 . सदिश संयोजन से क्या तात्पर्य है ?
उत्तर – दो या दो से अधिक सदिश जब किसी एक बिन्दु पर कार्यरत हों तो इन सभी सदिशों के सम्मिलित प्रभाव को केवल एक सदिश द्वारा व्यक्त करना सदिशों का संयोजन कहलाता है ।
प्रश्न 4 . सदिश संयोजन के समान्तर चतुर्भुज का नियम बताओ ।
उत्तर - यदि किसी बिन्दु पर दो सदिश एक साथ कार्य करें जो परिमाण तथा दिशा में समान्तर चतुर्भुज की दो संलग्न भुजाओं को प्रदर्शित करें , तो उनका परिणामी सदिश परिमाण तथा दिशा में विकर्ण ( Diagonal ) से प्रदर्शित होगा जो दोनों भुजाओं के कटान बिन्दु से होकर जाता है ।
प्रश्न 5 . सदिश राशियों के कुछ उदाहरण दीजिए ।
उत्तर - विस्थापन , वेग , त्वरण , संवेग , बल आदि ।
प्रश्न 6 . भार कैसी राशि है ?
उत्तर – सदिश राशि । क्योंकि यह वस्तु पर कार्यरत् गुरूत्वाकर्षण बल होता है ।
प्रश्न 7 . क्या द्रव्यमान भी सदिश राशि हैं ?
उत्तर - द्रव्यमान अदिश राशि है ।
प्रश्न 8 . प्रेक्षणों में भार को किस मात्रक में लिखते हैं ?
उत्तर - किग्रा भार या ग्राम भार में ।
प्रश्न 9 . ग्राम किसका मात्रक है ?
उत्तर - द्रव्यमान का ।
प्रश्न 10 ग्राम व ग्राम भार में क्या अन्तर है ?
उत्तर - ग्राम द्रव्यमान का तथा ग्राम भार बल का मात्रक है । ।
प्रश्न 11 . बल की परिभाषा दीजिए ।
उत्तर - बल वह धकेल अथवा खिंचाव है जो किसी वस्तु द्वारा दूसरी वस्तु पर लगाया जाता है ।
प्रश्न 12 . बल के क्या मात्रक हैं ?
उत्तर - बल के मात्रक न्यूटन ( SI पद्धति ) , डाईन ( CGS पद्धति ) किग्रा भार तथा ग्राम – भार ( दोनों गुरुत्वीय मात्रक )
प्रश्न 13 . 1 किग्रा भार कितने न्यूटन के बराबर होता है ?
उत्तर - 1 किग्रा भार = g न्यूटन = 9 . 8 न्यूटन
प्रश्न 14 . 1 ग्राम भार कितने न्यूटन के समान होता है ?
उत्तर - 1 ग्राम भार = 9.8 × 10-3 न्यूटन
प्रश्न 15 . एक न्यूटन बल से क्या अभिप्राय है ?
उत्तर - 1 न्यूटन बल वह बल है जो 1 किग्रा द्रव्यमान के पिण्ड में 1 मीटर / सेकण्ड2 का त्वरण उत्पन्न कर दे । ।
प्रश्न 16 . बल की विमाएँ बताइये ?
उत्तर - [MLT-2]
प्रश्न 17 . दो बलों
| → |
| F1 |
| → |
| F2 |
उत्तर - परिणामी बल F = √F12 + F22 + 2F1F2 cosθ
प्रश्न 18 . परिणामी बल का अधिकतम मान कितना होता है और कब होता है ?
उत्तर - अधिकतम मान F = F1 + F2 जबकि θ = 0° अर्थात् बल की एक ही दिशा में कार्यरत हों ।
प्रश्न 19 . परिणामी बल का न्यूनतम मान कितना होता है और कब होता है ?
उत्तर - न्यूनतम मान F = F1 - F2 जबकि θ = 180° अर्थात् बल विपरीत दिशाओं में कार्य कर रहे हों ।
प्रश्न 20 . संगामी बलों के संतुलन से आप क्या समझते हैं ?
उत्तर - संगामी बल संतुलन में होते हैं यदि सभी बलों का सदिश योग शून्य होता है ।
प्रश्न 21 . तीन बल , इस प्रकार हैं कि इनसे एक बन्द त्रिभुज की रचना होती है । बलों के संयोजन के सम्बन्ध में आप क्या कह सकते हैं ?
उत्तर - ये तीनों बल संतुलन में हैं ।
प्रश्न 22 . इस प्रयोग में घिरनियों में धर्षण होने से क्या हानि है ?
उत्तर - घिरनियों में घर्षण बल होने के कारण धागों में तनाव लटकाये गये भार से कम होंगे , जिससे परिणामी बल का मान कुछ कम आयेगा । ।
प्रश्न 23 . इस प्रयोग में धागे के स्थान पर धातु के तार का प्रयोग किया जा सकता है ?
उत्तर - नहीं , क्योंकि धातु का तार भारहीन तथा पूर्ण प्रत्यास्थ नहीं होता ।
प्रश्न 24 . क्या बलों के समान्तर चतुर्भुज का नियम वेगों के लिए भी सत्य है ?
उत्तर - हाँ , क्योंकि वेग भी एक सदिश राशि हैं ।
प्रश्न 25 . बलों के संतुलन का त्रिभुज का नियम बताइये ।
उत्तर - यदि किस बिन्दु पर एक साथ तीन बल कार्यरत हों तथा उन्हें परिमाण व दिशा में किसी त्रिभुज की चक्रीय क्रम में ली गयी भुजाओं द्वारा प्रदर्शित किया जा सके , तो वह बिन्दु संतुलन में होगा ।
प्रश्न 26 . त्रिभुज के नियम का व्यवहारिक उपयोग कहाँ है ?
उत्तर - पतंग उड़ाने में तथा तस्वीर टांगने में ।
प्रश्न 27 . धागे के नीचे निशान लगाने में समतल दर्पण की पट्टी का प्रयोग क्यों करते हैं ?
उत्तर – प्रतिबिम्ब की यथार्थ स्थिति ज्ञात करने के लिए ।
प्रश्न 28 . क्या यह उपकरण भार ज्ञात करने के लिए भौतिक तुला की भांति प्रयुक्त किया जा सकता है ?
उत्तर - नहीं , क्योंकि धिरनियों में कुछ न कुछ घर्षण अवश्य ही रहता है , अतः प्राप्त भार यथार्थ नहीं होता ।
