दो आवेशों के बीच पारस्परिक वैद्युत बल कूलॉम नियम द्वारा प्राप्त होता है । उस स्थिति में किसी आवेश पर आरोपित बल का परिकलन कैसे करें ? जहाँ उसके निकट एक आवेश न होकर उसे बहुत से आवेश चारों ओर से घेरे हों ? निर्वात में स्थित n स्थिर आवेशों q1 , q2 , q3 . . . . . qn के निकाय पर विचार कीजिए । q1 पर q2 , q3 , . . . . . qnके कारण कितना बल लगता है ? इसका उत्तर देने के लिए कूलॉम नियम पर्याप्त नहीं है ।
इसको समझने के लिए तीन आवेशों q1 ,q2 तथा q3 के निकाय पर विचार करें जिसको आगे चित्र में दर्शाया गया है । किसी एक आवेश जैसे q1 पर अन्य दो आवेशों q2तथा q3 के कारण बल को इनमें से प्रत्येक आवेश के कारण लगे बलों का सदिश संयोजन करके प्राप्त किया जा सकता है ।
इस प्रकार यदि q2 के कारण q1 पर बल को F12 द्वारा निर्दिष्ट किया जाता है , तो F12 को समीकरण दारा अन्य आवेशों की उपस्थिति होते हुए भी इस प्रकार व्यक्त किया जा सकता है-
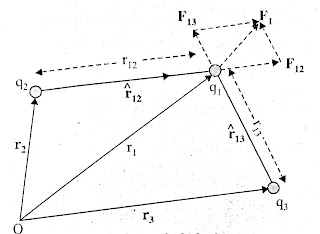 |
| चित्र A . तीन आवेशों के निकाय |
 |
| चित्र B . बहुल आवेशों के निकाय |
इसी प्रकार के कारण q3 पर लगा कूलॉम बल जिसे F13 द्वारा निर्दिष्ट करते हैं तथा जिसे लिख सकते हैं ।
यह भी q3 के कारण q1 पर लगा कूलॉम बल ही है जबकि अन्य आवेश q2 उपस्थित है । इस प्रकार q1 पर दो आवेशों q2 तथा q3 के कारण कुल बल F1 है ।
चित्र ( b ) में दर्शाए अनुसार तीन से अधिक आवेशों के निकाय के लिए उपर्युक्त परिकलन का व्यापकीकरण किया जा सकता है ।
अध्यारोपण के सिद्धान्त के अनुसार आवेशों q1 , q2 . . . . qn के किसी निकाय में आवेश q1 पर q2 द्वारा लगा बल कूलॉम नियम द्वारा लगे बल के समान होता है अर्थात् यह अन्य आवेशों q3 , q4 . . . . qn की उपस्थिति से प्रभावित नहीं होता । आवेश q1पर सभी आवेशों द्वारा लगा कुल बल F1 तब F12 , F13 . . . F1n का सदिश योग होगा । अतः
F1 = F12 + F13 + . . . + F1n
अतः उपर्युक्त व्यंजक ही बहुल आवेशों के बीच लगने वाले बल का व्यंजक है ।